Iniciar Sesión
Buenos Aires, 20/12/2025
AARON M. MCHAHON *
A continuación, exploro la naturaleza de los recursos de oro del mundo, particularmente la distribución de ley y la influencia que la geología regional y la cuasiología (proximidad a otros depósitos) ejercen sobre esas leyes.
Con la ayuda de un algoritmo de aprendizaje automático, creo una herramienta para predecir las calificaciones de oro que también expresa la incertidumbre en torno a esas predicciones. Esta herramienta solo requiere un par de coordenadas como entrada y el resto es automático.
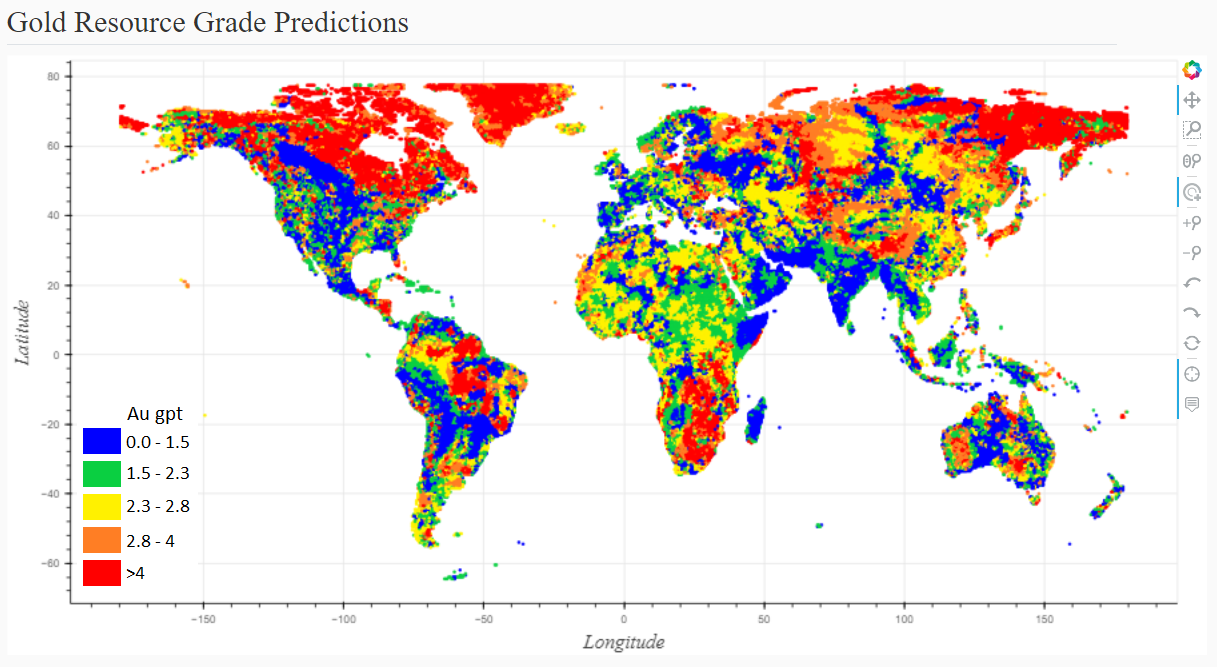
Finalmente, presiono las coordenadas para la mayor parte del mundo (excluidos los océanos y la Antártida) a través de la herramienta para producir este mapa interactivo (captura de pantalla a continuación).
Este trabajo proporciona contexto a las leyes de los recursos de oro, ayudándome a apreciar qué tan altos o bajos pueden llegar a ser según la ubicación.
Para este ejercicio, estoy extrayendo de tres conjuntos de datos: 1) MRDS, 2) GLiM y 3) Lith1.0. El MRDS es una base de datos compleja de depósitos minerales mundiales. Está disponible por el Servicio Geológico de los Estados Unidos y se actualizó por última vez en 2011. De la gran cantidad de información que se puede extraer, me centraré en algunas piezas clave. La primera pieza es grande: coordenadas.
Hay coordenadas para casi 300k depósitos únicos en todo el mundo con un sesgo notable hacia las Américas. Además de las coordenadas, también está disponible el producto principal de interés para cada uno de estos depósitos. Para alrededor de 7k depósitos, el MRDS incluye recursos minerales reportados, proporcionando toneladas y grado por producto. Mi enfoque está en aquellas propiedades con recursos.
GLim y Lith1.0 son mapas. GLiM es la abreviatura de Global Lithological Map (Hartmann y Moosdorf, 2012). Este es un mapa geológico unificado y simplificado del mundo convenientemente provisto como un Shapefile ESRI. Lith1.0 es un modelo del espesor litosférico a una resolución de 1 grado tanto en latitud como en longitud (Pasyanos et al., 2013). Ambos se muestran debajo superpuestos por el MRDS.
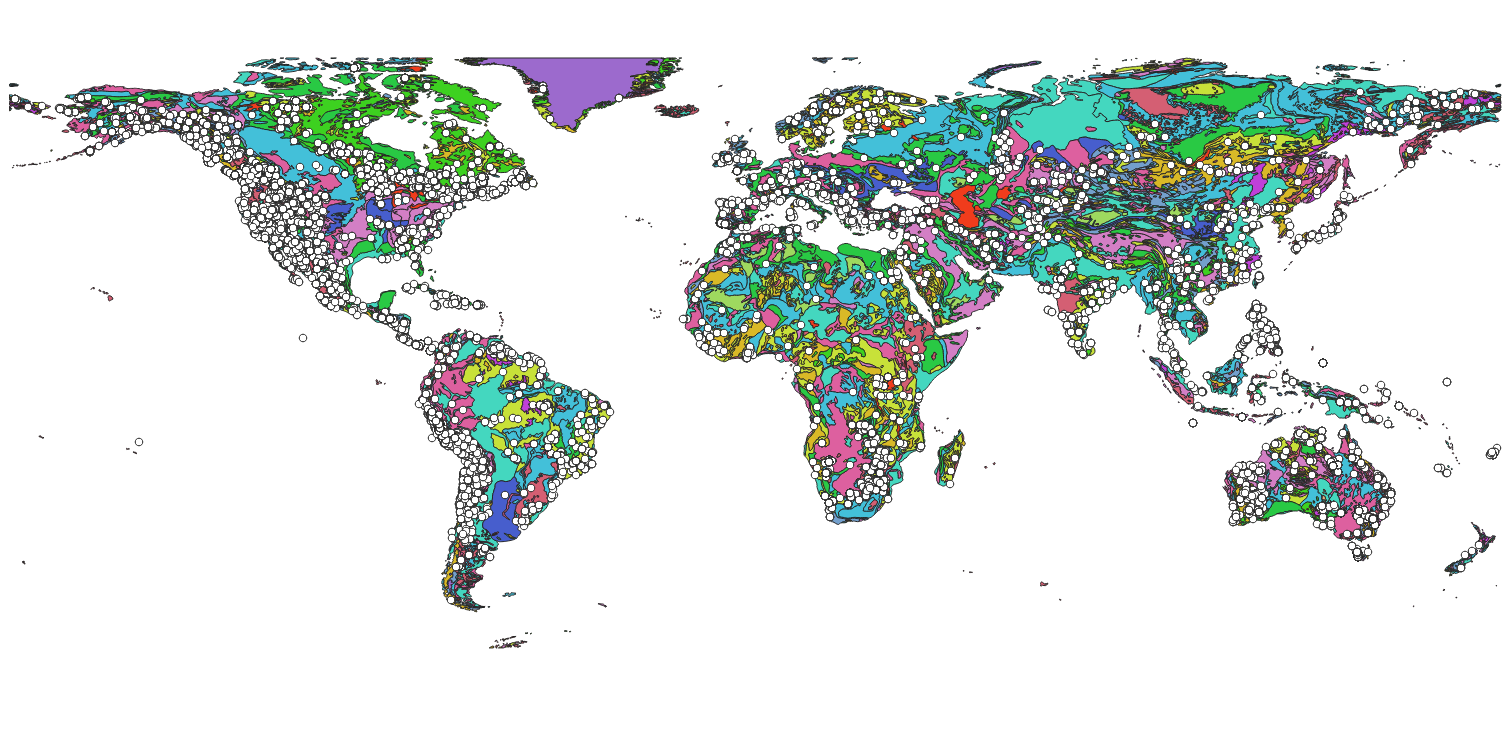
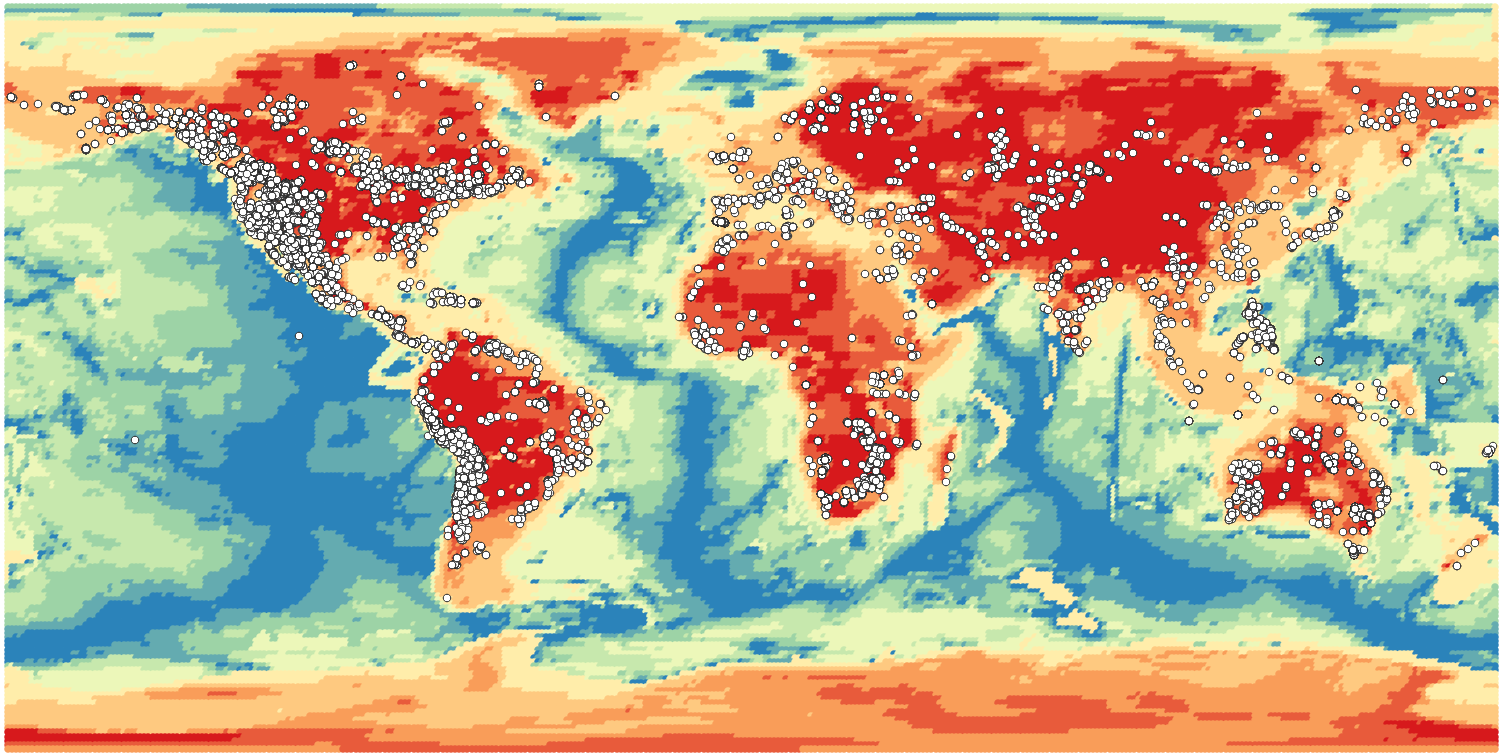
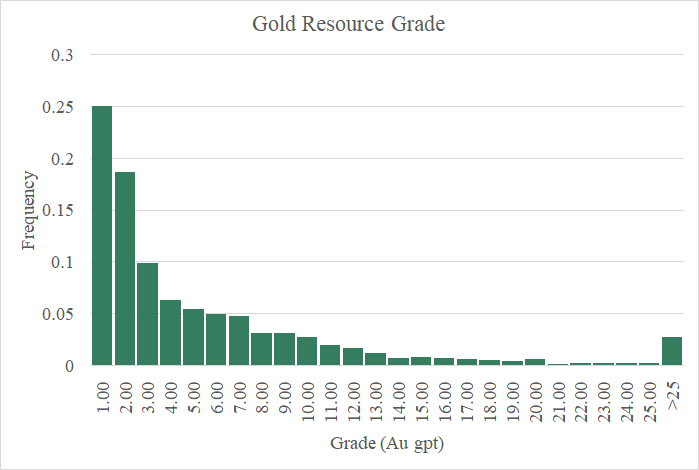
Echemos un vistazo a las calificaciones de estos recursos de oro en los cuadros a continuación. Puede ver que hay una considerable asimetría positiva en los datos.
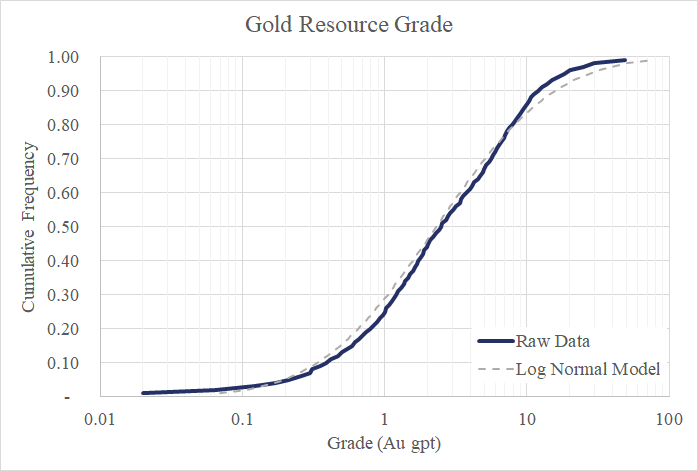
Desde la perspectiva proporcionada por el histograma (gráfico de barras verdes), es muy difícil discernir la naturaleza de la distribución con tantos valores amontonados en los tres primeros contenedores (0 a 3 Au gpt). La siguiente figura aclara un poco las cosas. Aquí estoy mostrando los mismos datos, pero he cambiado de un histograma a una curva de frecuencia acumulativa con una escala logarítmica para el eje X.
A primera vista, me parece que estos valores son parte de una distribución logarítmica normal que se comporta bien (es decir, los logaritmos naturales de estos valores están bien modelados por una distribución normal).
Mirando más de cerca la cola superior, particularmente los valores por encima del percentil 80, Sugiera que un modelo logarítmico normal para estos datos es un poco agresivo.
En otras palabras, los depósitos de oro de alta ley son menos probables de lo que predice un modelo logarítmico normal.
Esta distribución intensamente sesgada no es sorprendente dada la naturaleza de la mineralización. Demos un paso atrás y exploremos brevemente la distribución normal, que sirvió como base para todas las estadísticas que aprendí en la escuela.
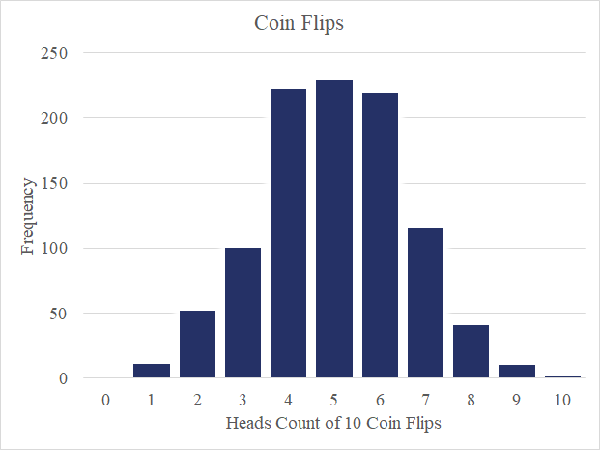
Según el teorema del límite central, puedo reproducir datos poco interesantes y distribuidos normalmente lanzando monedas. Por ejemplo, lanzo una moneda diez veces y registro el número de caras.
Repetido 1000 veces y trazando esos 1000 registros en un histograma, veo una bonita curva de campana como en esta figura. Por lo que sé de monedas, las probabilidades de que salga cara no se ven influenciadas por ninguno de mis lanzamientos de monedas anteriores. Dicho de otra manera, la moneda no tiene memoria.
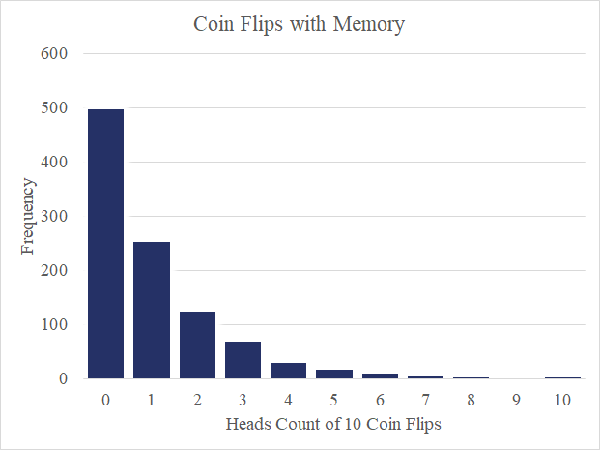
Ahora imagina que tengo una moneda mágica que recuerda el pasado. En el primer lanzamiento, todavía tengo probabilidades de que salga cara o cruz. Sin embargo, y aquí está la magia, la primera vez que lanzo cruz, las probabilidades cambian de modo que la moneda solo devolverá cruz durante el resto de la ronda.
La moneda recuerda. Un histograma de 1000 rondas en este escenario que se muestra a continuación nos da una distribución sesgada positivamente que recuerda a nuestros datos de ley de oro.
Creo que la idea clave aquí es que los sistemas de mineralización tienen memoria. Las condiciones que permiten que una ampolla de sulfuro cargado de oro se nuclee en una determinada parte del mundo, persisten o permanecen en la memoria durante un tiempo, lo que permite una nucleación adicional.
Además, la mera presencia de un mineral proporciona sitios de nucleación atractivos, lo que aumenta significativamente las probabilidades de una mayor mineralización del mismo. Estos tipos de sistemas de composición o multiplicación producen los resultados altamente sesgados que encontramos en los datos de ley de oro.
Nuevas características
La naturaleza de la distribución de la ley de oro es interesante y comienza a enfocar mi intuición sobre la ley de oro relativa y lo que realmente queremos decir con alta y baja ley. Sin embargo, todavía tenemos que considerar la geografía.
Después de todo, lo que es de alta ley para un depósito de oro en Nevada no es lo mismo que en el Escudo Canadiense. En otras palabras, hay características geográficas de estos depósitos además del grado que vale la pena conocer.
He aquí por qué las coordenadas son tan importantes. Con ellos, puedo agregar los datos de ley de oro con todo tipo de características geográficas nuevas. Haciendo una referencia cruzada de las ubicaciones de los depósitos con el mapa geológico GLiM del mundo, agrego litología generalizada al conjunto de datos. Hago lo mismo con el conjunto de datos Lith1.0 para el espesor de la litosfera.
¿Y la cuasiología? La cuasiología es solo una palabra clave más accesible para la geoestadística. En resumen, la cuasiología intenta identificar y extraer cualquier información útil sobre, en este caso particular, la ley de un recurso de oro de los recursos vecinos.
Para hacer eso, construyo algunas características nuevas para agregar al conjunto de datos. Primero, es una puntuación en la que calculo la distancia inversa de un recurso a todos los demás recursos en el conjunto de datos y los resumo todos.
Los recursos con una puntuación alta tienen un gran número de vecinos cercanos. El segundo toma esas mismas distancias inversas y las multiplica por los grados de recursos vecinos (de hecho, una ponderación de distancia inversa) y suma esos valores. La tercera y cuarta características son las mismas que la primera y la segunda, pero con un toque.
Solo los recursos vecinos con la misma mercancía (oro en este caso) se incluyen en las sumas. Ahora, tenemos cuatro características nuevas, cada una de las cuales tiene una visión ligeramente diferente de la cuasiología. Ahora es el momento de hacer un buen uso de esas funciones.
Aprendizaje automático
De todas estas excelentes características, ¿cuál, si alguna, tiene más poder para predecir la ley de un recurso de oro? El algoritmo RReliefF puntúa características para ese propósito y para nuestro conjunto de datos recién agregado, las cinco características principales son la profundidad de la litosfera y mis cuatro características casi lógicas. Dicho esto, los extensos datos de litología que adjunté todavía hacen una contribución positiva al resultado final.
El siguiente paso es entrenar un algoritmo para producir un modelo predictivo y evaluar la precisión de ese modelo. Después de un poco de experimentación, elegí el algoritmo AdaBoost (regresor usando árboles de decisión) para la tarea. Su trabajo es identificar las relaciones entre las leyes de los recursos de oro y sus datos de características correspondientes.
A través de un método llamado Validación cruzada de 5 veces, oculto iterativamente 1/5 de los datos del algoritmo, le permito producir un modelo predictivo a partir de los datos restantes, alimentar los datos de características ocultas a través del modelo recién producido y luego comparar el modelo predicciones de ley de oro con los valores conocidos. Esto se repite de manera que cada quinto de los datos tenga un turno oculto.
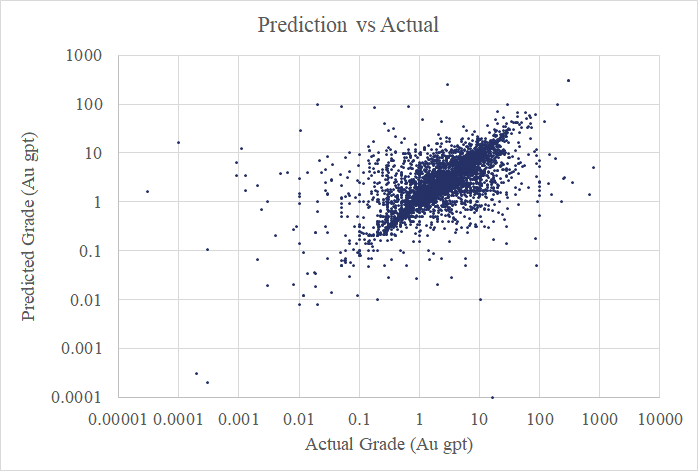
Entonces, ¿cómo funcionan los modelos producidos por este algoritmo? ¡No está mal! A continuación se muestra un diagrama de dispersión de mi ejercicio de validación cruzada de 5 veces. Cada punto traza el grado real de uno de los recursos de oro en el conjunto de datos contra su grado predicho (cuando estaba oculto al algoritmo).
Todavía hay mucho ruido allí, pero también algo de señal. Hemos visto la alta variabilidad en los datos de ley de oro en los gráficos anteriores. El algoritmo me está dando modelos que pueden explicar aproximadamente el 40% de esa variabilidad *.
*Estoy haciendo esta afirmación después de usar una transformación de Box-Cox para reformar los datos en una distribución casi gaussiana y comparar la desviación media absoluta de las calificaciones reales y pronosticadas.
Herramientas útiles
Estoy proporcionando acceso a mi modelo predictivo para las leyes de los recursos de oro a través de dos herramientas. El primero requiere que el usuario ingrese cualquier par de coordenadas mundiales en grados de longitud y latitud.
A continuación se muestra un ejemplo de un par de coordenadas en el centro de Nevada. Las características geográficas (es decir, geología, litología, profundidad de la litosfera y puntuaciones de cuasiología) se calculan automáticamente para esa ubicación en particular y se alimentan a través del modelo predictivo.
La salida es un par de curvas de frecuencia acumuladas. Uno es simplemente la distribución de frecuencia de los datos MRDS sin procesar para las leyes de recursos de oro ('Sin procesar') como referencia. El otro es la distribución de frecuencia prevista para las coordenadas proporcionadas ('Modelo ML').
Aquí hay algunos números notables del modelo ML: el percentil 25 es 1.4 gpt, el 50 es 3.1 gpt y el percentil 90 es 11.2 gpt. De acuerdo, son muchos números, pero permítanme ir un poco más allá y ser más explícito sobre lo que significa esta distribución de frecuencia predicha para mí: si existiera un recurso de oro en esta ubicación y el Servicio Geológico de EE.UU. para incluirlo en el MRDS, le doy una posibilidad entre cuatro de tener una calificación superior a 1,4, una posibilidad entre dos de tener una calificación superior a 3,1 y una posibilidad entre diez de superar los 11,2 gpt.
El percentil 50 es el valor de salida de mi modelo predictivo. La forma de la distribución (no del todo logarítmica normal) fue una llamada subjetiva que hice después de jugar con los datos sin procesar.
Puedo ser aún más explícito, pero primero es mejor que vuelva a presentar la segunda herramienta, que es mi mapa de grado dorado del mundo. Una vez configurado un sistema para usar el modelo predictivo con solo proporcionar un par de coordenadas, lo siguiente que debe hacer es introducir todas las coordenadas del mundo en el modelo y trazar las predicciones en un mapa. Hacerlo (ignorando los océanos y la Antártida) me da este mapa, que mostré anteriormente.

Es muy tentador para mí concluir, basándose en este mapa, que la geología y la cuasiología del norte de Canadá lo convierten en un gran lugar para buscar depósitos de oro. Ahora, creo que eso es cierto, pero hay un elemento humano capturado en este mapa que debe ser apreciado.
Dado que estos son los datos del Servicio Geológico de EE.UU. con los que estoy trabajando, sospecho que los depósitos de baja ley están mejor representados en los EE.UU. que en otras regiones. Esto reduciría mis expectativas de calificaciones modeladas para los EE.UU.
Además, puede ser costoso trabajar en el norte de Canadá u otras regiones frías, de modo que los humanos no están interesados en hacer mucho trabajo informando recursos para depósitos de menor ley allí, filtrándolos efectivamente del conjunto de datos. Un filtrado similar podría ocurrir en regiones donde los depósitos son profundos y requieren mayores costos para explotarlos.
Dejando a un lado la pereza humana, también es importante señalar que este mapa no expresa la probabilidad de ubicar un recurso, solo establece expectativas de calificación condicionadas a un recurso existente.
* Geólogo, fundador de Tacit Vision LLC. Creador de herramientas de inteligencia artificial útiles para la toma de decisiones en la industria minera